|
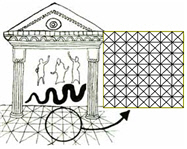 |
| 고대 그리스 신전 |
필자는 수학사에 가장 위대한 순간으로 하나를 꼽으라면 주저 없이 이 피타고라스정리의 발견을 택합니다. 왜냐면 이 발견에 의해서 수백 년 넘게 믿어왔던 수학과 철학의 사고가 무너졌으며 수학의 획기적인 발전을 이루었기 때문입니다.
고대 그리스 철학에서는 다음과 같은 전제가 있었습니다. "임의의 두 선분은 같은 단위로 측정할 수 있다. 즉 공통 측정단위를 갖는다." 이 전제를 기반으로 그리스인들은 수학과 철학의 사고를 전개해 나갔습니다. 그리고 이 전제에 따르면 모든 존재하는 수들은 유리수(rational number, 두 자연수의 비(ratio)을 나타내는 수)였습니다. 왜냐면 임의의 양수 x에 대해서, 위 전제를 양수 x와 1에 적용하면 공통 측정단위인 y가 존재하여 x=ny, 1=my (x는 y의 n배, 1은 y의 m배)로 나타낼 수 있습니다. 이로부터, y=1/m이고 따라서 x=ny=n/m이 되어 x는 유리수가 되기 때문이었습니다.
그런데 피타고라스의 정리에 의하면 한 변이 1인 정사각형의 대각선의 길이는 제곱하면 2가되는 수 (이 수를 로 나타냄)이며 이 수는 유리수가 아님을 깨달게 되었습니다. 즉 우리의 세상에 유리수가 아닌 수, 즉 무리수의 존재를 인식하게 된 순간입니다. 하지만 피타고라스는 위대한 발견을 세상에 알려 개인의 명성을 얻기보단 학자의 사회적 책임을 보다 중시하여 이로 인해 야기되는 사회적 혼란을 막기 위해 세상에 이 사살을 알리지 못하도록 함구령을 내렸
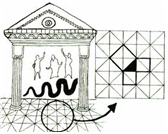 |
| 피타고라스 정리 |
이 직각삼각형 세 변들의 관계는 피타고라스 시대보다 1000년 이상의 이전인 고개 바빌로니아에서도 이미 알고 있었으며 피타고라스 이전은 아닐지라도 고대 인도나 중국의 문헌에도 나타납니다. 현재까지 피타고라스 정리의 증명법은 200가지가 넘으며, 미국의 20대 대통령인 제임스 가필드도 사다리꼴을 이용해 이 정리를 증명했습니다. 그런데 이 정리에 피타고라스의 이름을 붙인 이유는 피타고라스학파에 의해서 그 사실이 처음으로 증명됐기 때문입니다. 사실 무엇을 안다는 것과 그 것을 증명하는 것은 전혀 다른 이야기입니다. 그래서 우리는 수학을 통해서 여러 가지 이론이나 사실들을 배우지만 근본적으로 자신의 생각이나 주장을 논리적으로 전개하고 설명하는 힘을 배우는 것입니다.
그런데 피타고라스는 위 신전의 바닥문형을 보고 이 정리를 발견했다고 전해집니다. 그렇다면 저 신전은 수많은 사람들이 지나다녔을 것인데, 왜 피타고라스만이 이 사실을 깨달았을까요? 그 이유는 피타고라스는 길이와 넓이와의 관계 등 도형의 성질에 대해서 알고 있었기에 위 그림처럼 그 문향 속에서 숨겨진 직각삼각형과 그 변을 한 변으로 하는 정사각형들이 보였던 것이지요. "우리는 아는 만큼 느끼고, 느낀 만큼 보인다."라는 어느 학자의 말을 우리는 절실히 공감하게 됩니다.
윤강준 국가수리과학연구소 산업수학전략연구부장
중도일보(www.joongdo.co.kr), 무단전재 및 수집, 재배포 금지
 김성현 기자
김성현 기자