통계학의 난제 ‘차원의 저주’ 풀었다

박병욱 서울대 교수 연구팀 성과
비모수적 방법론 활용 가능해져
세계 통계학계에서도 주목

통계학의 회귀분석에서 최대 난제인 ‘차원의 저주’가 드디어 풀렸다.

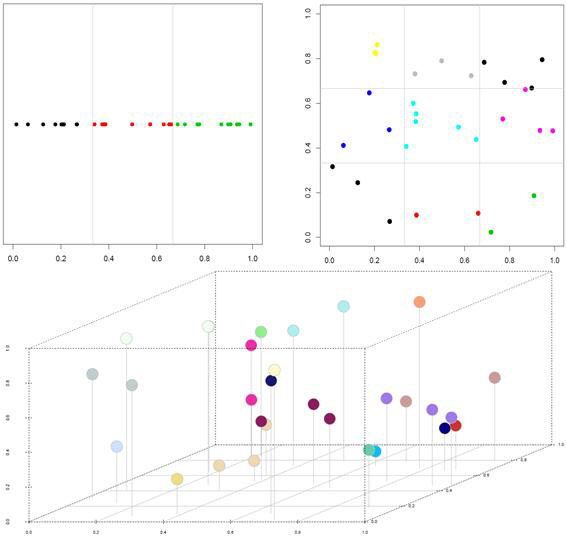
박병욱 서울대 교수 연구팀은 구조화 비모수모형의 추정을 통해 차원의 저주를 해결하는 방법론을 개발했다고 한국연구재단이 밝혔다.

통계학에서는 관측된 자료를 바탕으로 여러 변수 간의 관계를 추정해 낸다. 그중 비모수적 방법론은 변수 간의 함수가 무한 차원일 수 있다고 가정해 더 정확한 관계식을 추정한다. 그러나 변수의 개수에 비례해 추정의 정확도가 떨어지는 현상인 차원의 저주를 피하지 못해 실제 활용도가 제한적이다.

연구팀은 함수에 특별한 구조를 가정하고 함수를 추정한 뒤, 적절한 알고리즘을 적용하면 차원의 저주를 피할 수 있음을 규명했다.

대표적인 구조로는 가법구조, 부분선형가법구조, 변수계수구조 등이 있고, 해당 구조들은 여전히 함수가 무한 차원임을 허용하는 구조라는 점에서 희미가 있다.

통계학계에서도 이 연구에 대한 지대한 관심을 보이고 있다. 제28차 세계수학자대회에서 박병욱 교수에게 발표를 요청해 왔다. 한국 통계학자는 박병욱 교수가 최초다.

박병욱 교수는 “향후 유클리드 공간에 속하는 자료를 넘어 최근 대두하는 이미지 자료, 형상 자료, 함수 자료 등 비유클리디안 자료도 분석할 수 있는 비모수구조모형을 연구할 계획”이라고 밝혔다.
이해미 기자 ham7239@